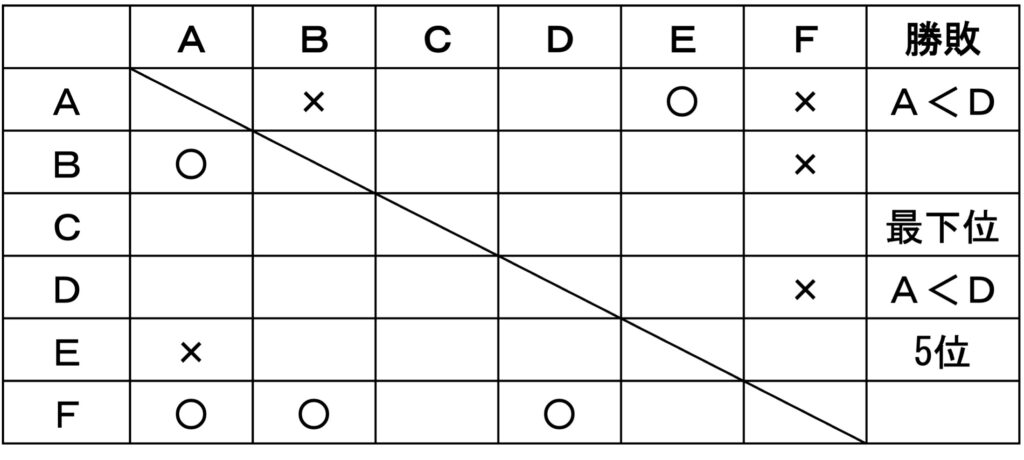
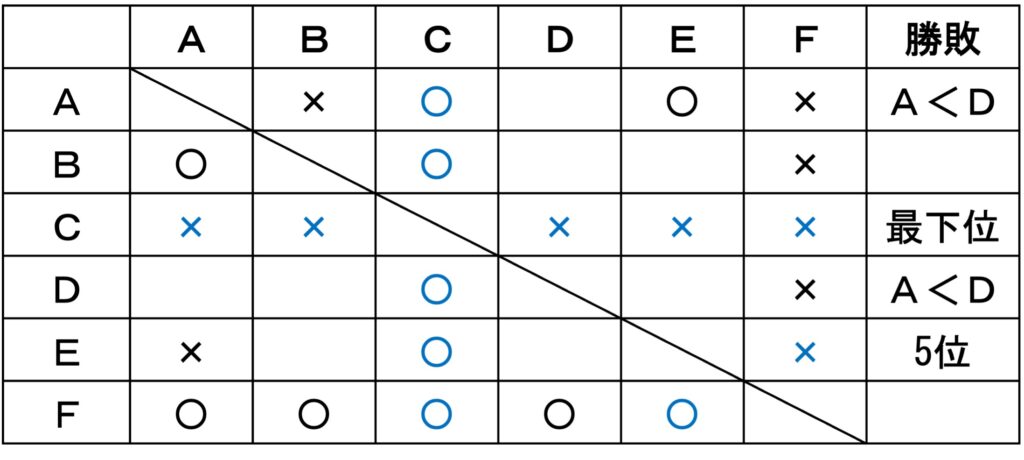
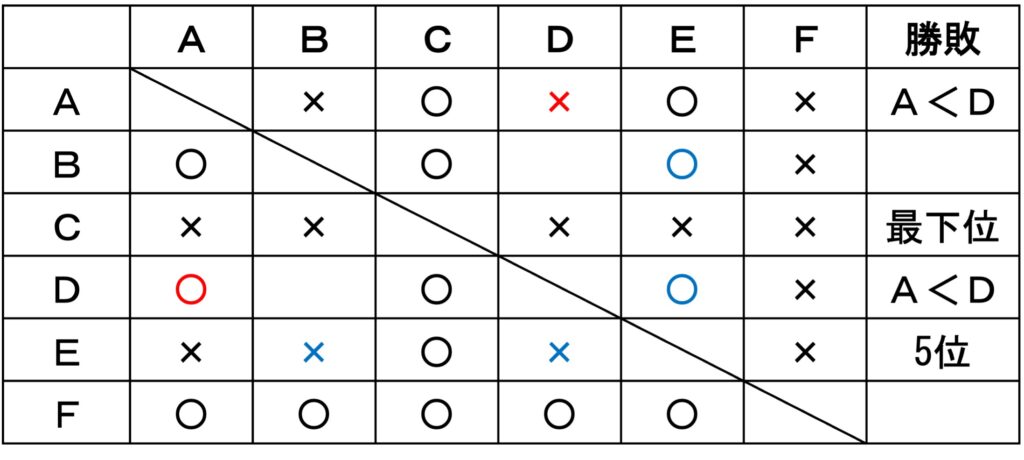
公務員試験合否のカギとなる「知能分野」について解法と過去問題集を電子書籍で配信します。

知能分野では「数的推理」と「判断推理」が重要な科目となります。こちらのサイトでは、「数的推理」と「判断推理」を合わせて「数的処理」としています。
初めて学習する方に向けて、知能分野を得意になるための情報を書籍にしていきます。
①「数的処理を確実に速く解く方法」:解法をパターン別に解説した導入書です。問題ごとの解法パターンを紹介します。
②「数的推理大全」:数的推理の過去問題を試験レベル別に分けて解説しています。
③「判断推理大全」:判断推理の過去問題を試験レベル別に分けて解説しています。
〔レベル分け〕
上級:国家公務員一般職(大卒)、国家公務員専門職、裁判所(大卒)、都道府県職員(上級)等
中級:市役所職員(大卒)、警察官(大卒)、消防官(大卒)等
初級:国家公務員一般職(高卒)、地方初級、資格職(保育士、栄養士、理学療法士等)
2026年1月刊行・配信予定です
問題集配信までは「問題演習」をご利用ください。
問題演習では、最近出題された知能問題を少しずつアップしていきます。