最近出題された判断推理の解説です。
「暗号」
〔問題〕ある暗号で「アオイ」が「0121 1061 0142」、「ヒカルゲンジ」が「2442 1110 7274 9395 5610 8586」で表されるとき、同じ暗号の法則で「1263 7674 1663 2153」と表されるのはどれか。
1 「ウツセミ」
2 「カシワギ」
3 「スズムシ」
4 「ハシヒメ」
5 「ユウギリ」
「試合(総当たり戦)」
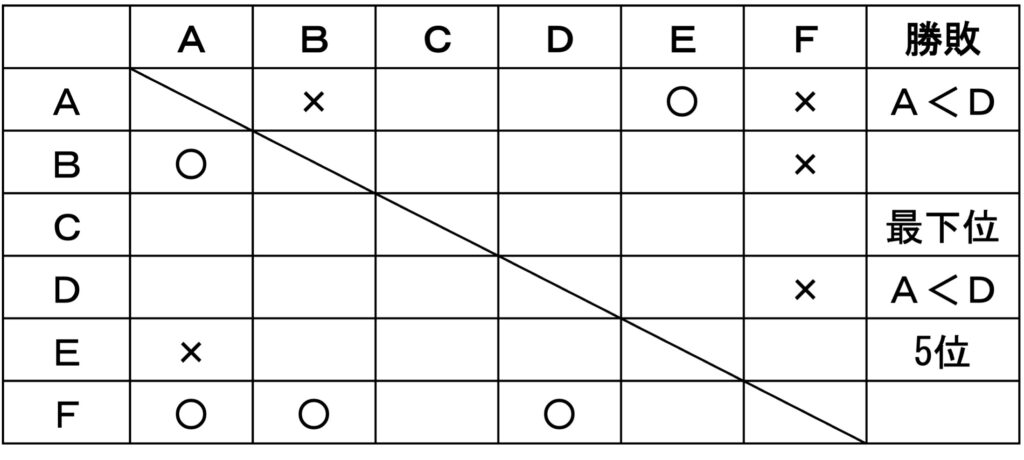
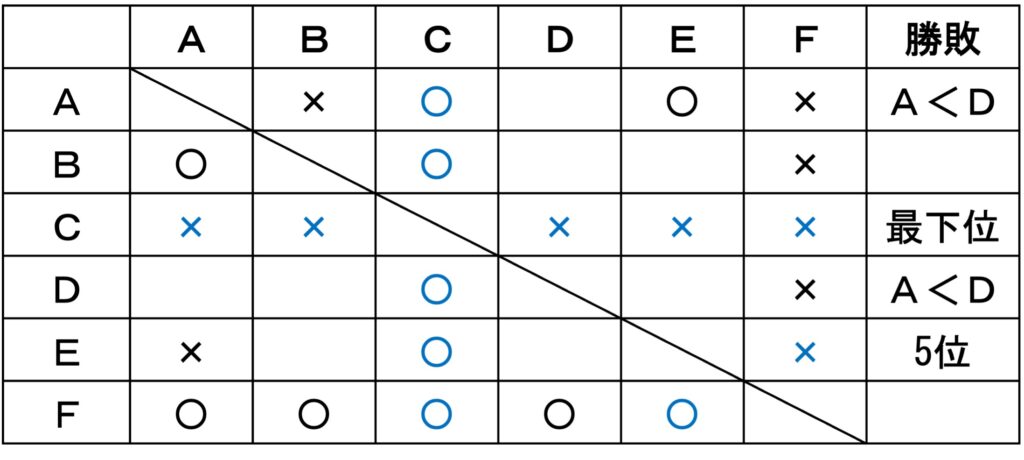
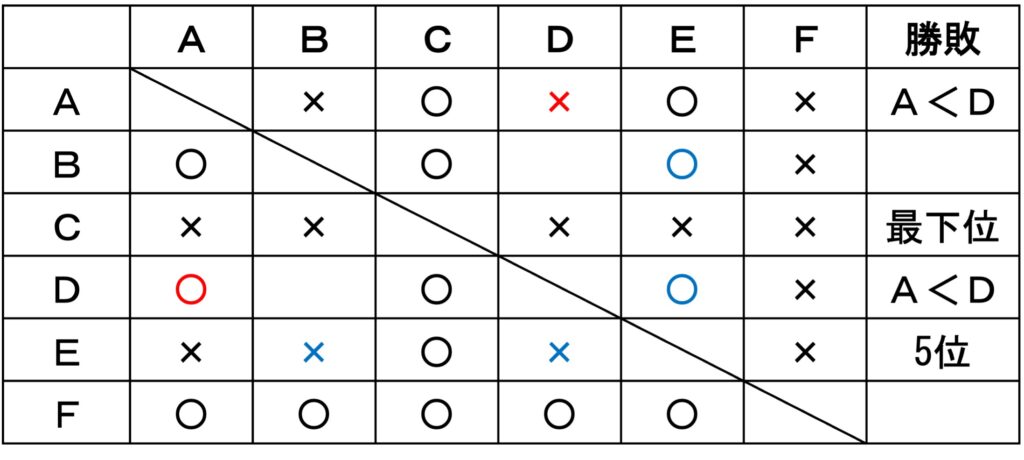
〔 問題〕A〜Fの6人が卓球の総当たりの個人リーグ戦を行った結果、次のア〜オのことがわかっているとき、確実にいえるのはどれか。ただし、引き分けの試合はなく、同じ順位の者のいなかったものとする。
ア AはBとFに負けた。
イ AはDより順位が低かった。
ウ EはAに負け5位だった。
エ FはBとDに勝った。
オ Cは最下位だった。
1 Aは4位だった。
2 BはDに勝った。
3 BはEに負けた。
4 Dは3位だった。
5 Fは2位だった。
「集合」
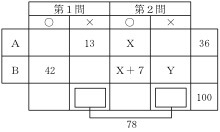
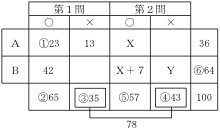
〔 問題〕あるテレビ番組のクイズ大会に参加したA大学及びB大学の計 100人の学生について、出題された第1問及び第2問の2題のクイズへの解答状況を調べたところ、次のア~カのことが分かった。
ア クイズ大会に参加したA大学の学生の人数は、 36人であった。
イ 第1問を正解したB大学の学生の人数は、 42人であった。
ウ 第1問が不正解であったA大学の学生の人数は、 13人であった。
エ 第1問が不正解であった学生の人数と第2問が不正解であった学生の人数との和は、延べ 78人であった。
オ 第2問を正解した学生の人数は、B大学の学生がA大学の学生より7人多かった。
カ クイズ大会に参加した学生の全員が、第1問及び第2問の2題のクイズに答えた。
以上から判断して、第2問が不正解であったB大学の学生の人数として、正しいのはどれか。
1. 28人
2. 29人
3. 30人
4. 31人
5. 32人
「試合」(トーナメント戦)
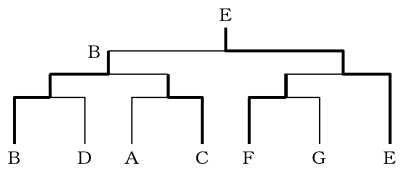
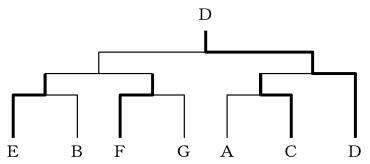
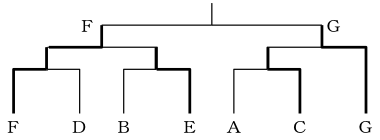
〔問題〕ある剣道大会で、A~Gの7チームが、下図のようなトーナメント戦を行った結果について、次のア~エのことが分かった。
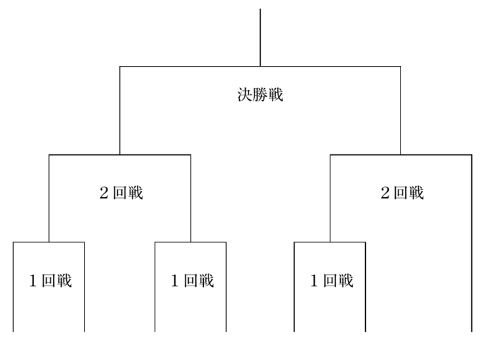
ア AはCに負けた。
イ BはEに負けた。
ウ FはEと対戦した。
エ FはGに勝った。
以上から判断して、確実にいえるのはどれか。
1 Aは決勝戦に進んだ。
2 Bが決勝戦に進んだとすると、FはGと2回戦で対戦した。
3 Dが優勝したとすると、DはCと対戦した。
4 FはEと1回戦で対戦した。
5 Gが決勝戦に進んだとすると、BはDと対戦した。
「ウソつき+順序」
〔問題〕A~Eの5人が、登山をしたときに山項へ到着した順番について、それぞれ次のように発言している。5人の発言の一方は事実であり、他方は事実ではない。最初に到着した人として、正しいのはどれか。ただし、同着はないものとする。
A 「私はDの次に到着した。」 「CはEの次に到着した。」
B 「私はEの次に到着した。」 「Aは最後に到着した。」
C 「私はBの次に到着した。」 「EはDの次に到着した。」
D 「私は最後に到着した。」 「BはEの次に到着した。」
E 「私はAの次に到着した。」 「AはCの次に到着した。」
1 A
2 B
3 C
4 D
5 E
「論理」
〔問題〕あるクラスで国語、数学、理科、社会、英語について、得意かどうかのアンケートを実施したところ、次のア~ウのことが分かった。このとき、確実に言えることとして、最も妥当なのはどれか。
ア 英語が得意でない人は、国語が得意である。
イ 数学が得意な人は、社会が得意かつ国語が得意でない。
ウ 社会または英語が得意な人は、理科が得意でない。
(1) 英語が得意な人は国語が得意でない。
(2) 国語が得意な人は理科が得意でない。
(3) 数学が得意な人は理科が得意である。
(4) 理科が得意な人は数学が得意でない。
(5) 社会が得意な人は数学が得意である。
「数からの推理」
〔問題〕6つの商業施設A~Fについて、所在地と業態分類を調べたところ、以下のことが分かった。確実にいえるのはどれか。
ア A、B、C、Dのうち、東京にあるものは2つであり、百貨店は2つである。
イ B、C、D、Eのうち、東京にあるものは1つであり、百貨店は2つである。
ウ C、D、E、Fのうち、東京にあるものは2つであり、百貨店は1つである。
1 Aは、東京にあるが、百貨店ではない。
2 Cは、東京にはないが、百貨店である。
3 Dは、東京にあるが、百貨店ではない。
4 Eは、東京にはないが、百貨店である。
5 Fは、東京にあるが、百貨店ではない。
「集合」
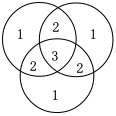
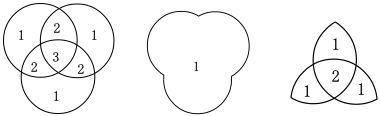
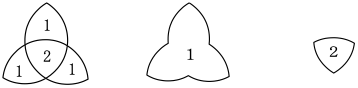
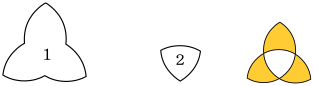
〔問題〕来日2度目の外国人観光客200人に、東京、大阪、福岡のうち、前回の来日で訪れたことがある都市についでアンケートをとったところ、次のア~オのことが分かった。このとき、東京、大阪、福岡のうち2都市だけを訪れたことがある者の人数として、最も妥当なのはどれか。
ア 東京を訪れたことがあると答えた者は120人であった。
イ 大阪を訪れたことがあると答えた者は92人であった。
ウ 福岡を訪れたことがあると答えた者は72人であった。
エ 3都市のどれも訪れたことがないと答えた者は20人であった。
オ いずれか1つの都市だけ訪れたことがあると答えた者は100人であった。
(1) 46人
(2) 48人
(3) 56人
(4) 58人
(5) 66人