市役所試験の要項チェック
7月1日には発表の遅い市役所も、試験要項を発表します。
受験を希望する市役所のホームページから「職員採用試験」と検索して、今年度の試験要項を確認してください。
令和7年度では、多くの市役所が、通常の公務員試験ではなく、SPIやSCOAといった民間企業で実施される採用試験を利用しています。
この場合は市販の対策本で対応可能です。
通常の公務員試験でも知能重視の採用試験に変えている所もありますので、科目や出題数に注意してください。
7月1日には発表の遅い市役所も、試験要項を発表します。
受験を希望する市役所のホームページから「職員採用試験」と検索して、今年度の試験要項を確認してください。
令和7年度では、多くの市役所が、通常の公務員試験ではなく、SPIやSCOAといった民間企業で実施される採用試験を利用しています。
この場合は市販の対策本で対応可能です。
通常の公務員試験でも知能重視の採用試験に変えている所もありますので、科目や出題数に注意してください。
〔解説〕正答3
4桁の数字と文字数が同じなので、4桁の数字が一文字を表していることがわかる。
アとイが一つ違いなので50音表を当てはめて考える。
ただ、同じア行のオが「01」からではなく「10」から始まっているのでア行が「01」と決まっているわけではないことがわかる。
前半は行、後半は何番目かを表していると考えて進めてみる。
そして、前半は足し算、後半は引き算で順番を表していると気づければこの問題は解ける。
ア:0+1=1(1行目)、2−1=1(1番目)
オ:1+0=1(1行目)、6−1=5(5番目)
イ:0+1=1(1行目)、4−2=2(2番目)
ヒ:2+4=6(6行目)、4−2=2(2番目)
カ:1+1=2(2行目)、4−2=2(2番目)
ル:7+2=9(9行目)、7−4=3(3番目)
ゲ:9+3=12(濁点なので10増えていると考える)→(2行目)、9−5=4(4番目)
ン:5+6=11(11行目)、1−0=1(1番目)
ジ:8+5=13(濁点なので10増えていると考える)→(3行目)、8−6=2(2番目)
問題は、
1+2=3(3行目)6−3=3(3番目)→ス
7+6=13(濁点なので3行目)7−4=3(3番目)→ズ
1+6=7(7行目)6−3=3(3番目)→ム
2+1=3(3行目)5−3=2(2番目)→シ
「スズムシ」となり選択肢3が正解となる。
〔解説〕正答 1
「引き分け、同順位がない」ということは、5勝0敗から0勝5敗まで勝敗がきれいに分かれるということである。
条件を表に記入すると次のようになる。
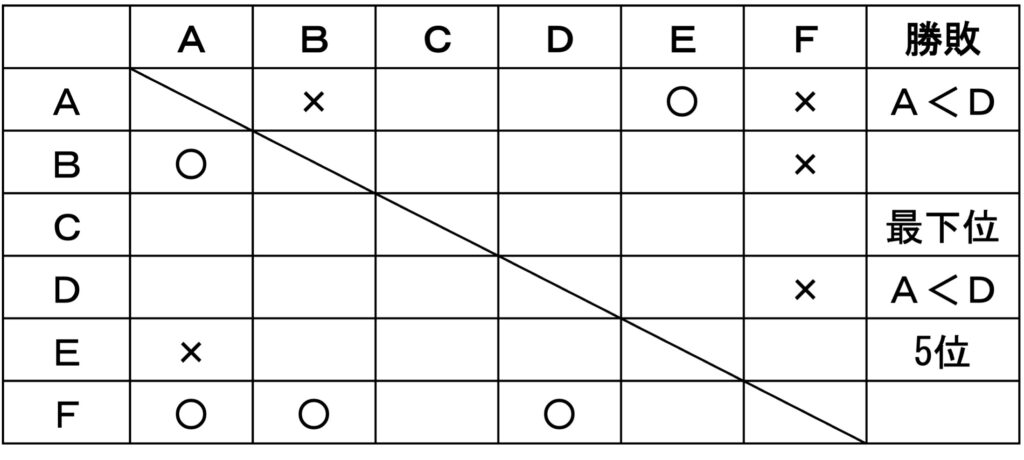
Cは最下位とわかっているので0勝5敗、全勝の5勝0敗はF。
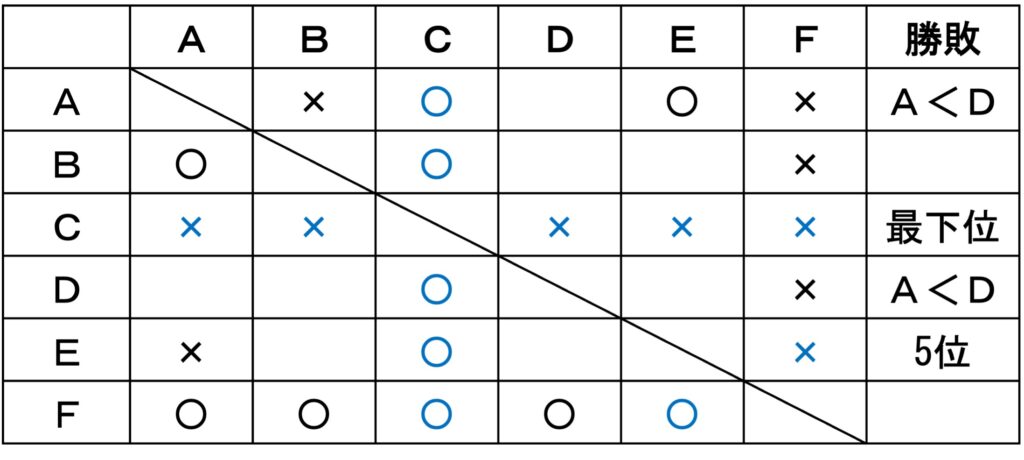
Eは5位なので1勝4敗であり、C以外の対戦は全て負けとなる。AはDより下位なのでDとの対戦は負け。
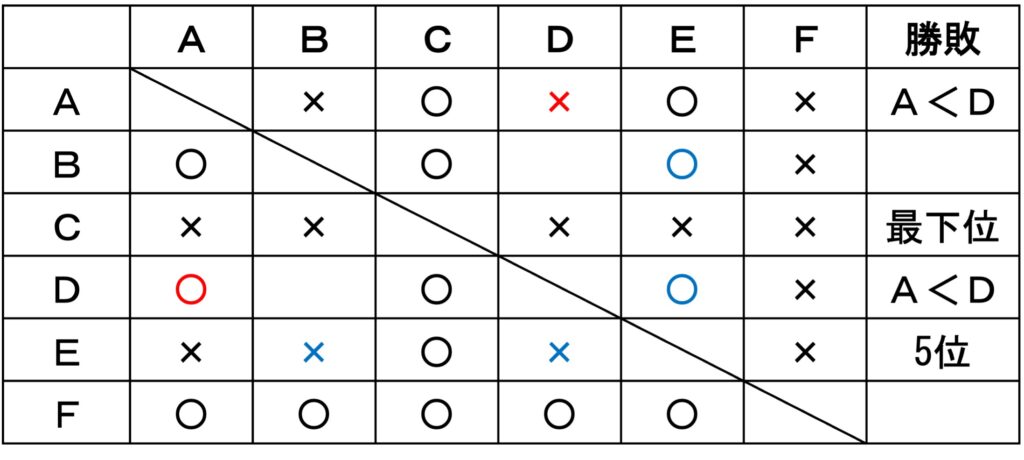
BとDの対戦は情報がないので、どちらが勝ったかは不明となる。この状態で選択肢を検討する。
確実に言えるのは、Aが2勝3敗で2位の選択肢1となる。
〔解説〕
一定の距離にかかる歩数と歩幅は逆比となる。「歩幅×一定時間に歩く歩数」が速さとなる。
同じ距離を進む歩数は、親と子で2:5なので、歩幅は5:2となる。
1秒間に歩く歩数は親と子で2:4なので、親と子の速さは(5×2):(2×4)=10:8=5:4である。
したがって子が3秒歩いている距離は4×3=12
親が追いつくまでにかかる時間は12÷(5−4)=12
したがって、子供が歩きはじめてからかかる時間は3+12=15(秒後)となる。
〔正答 4〕
9枚のカードから3枚を取り出す場合の数は、9C3=9×8×7 /3×2×1 =84(通り)
次に、3枚のカードの合計が6の倍数となるケースを考える。
合計が6の場合:(3,2,1) 1通り
合計が12の場合:(9,2,1)(8,3,1)(7,4,1)(7,3,2)(6、5,1)(6,4,2)(5,4,3) 7通り
合計が18の場合:(9,8,1)(9、7,2)(9,6,3)(9,5,4)(8,7,3)(8,6、4)(7,6,5) 7通り
合計が24の場合:(9,8,7) 1通り
合計16通りとなる。
したがって、3枚のカードの和が6の倍数となる確率は、16/84 =4/21 となる。
〔解説〕正答 3
ア〜オの条件をベン図で表すと次のようになる。求める形になるように必要ない部分を削除していく。
以下計算式と図の形を追っていく。図の中の数値はその部分が何回計算されているかを示している。

200-20=180
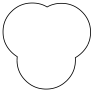
180 - 100 =80

120+92+72=284
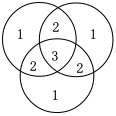
284 - 180 = 104
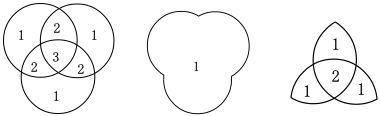
104 - 80 = 24
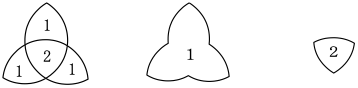
80 - 24 =56
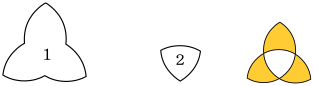
〔解説〕正答 4
命題を記号化すると次のようになる。バーは否定形を表す。
ア 英→国
イ 数→社かつ国
ウ 社または英→理
与えられた命題の対偶は必ず正しいので対偶を求める。
これらの対偶は次の通りとなる。選択肢ごとに命題が矢印でつながるかを確認する。
ア 国→英
イ 社または国→数
ウ 理→社かつ英
1.英→つながらない。
2.国→つながらない。
3.数→社かつ国→つながらない。
4.理→社 →数 したがって、理→数 となる。正しい。
かつ英 →国
5.社→理 これ以降つながらない。
〔解説〕正答 5
まず、所在地(東京にあるもの)について考える。条件アより、A~Dのうち東京にあるものを、A・Bと仮定する。すると、条件イより、B~Eのうち東京にあるのは、Bとなる。さらに、条件ウより、C~Fのうち東京にあるのは、Fのみとなってしまう。これは、条件ウに反する(C~F-東京=2)。
また、条件アより、A~Dのうち東京にあるものを、B~Dの中で決めるのも、条件イに反する(B~E-東京=1)。
したがって、条件ア~ウより、東京の可能性があるのは、「A・C・F」もしくは、「A・D・F」となる(C・Dは確実ではない)。
次に、業態分類について考える。条件アより、A~Dのうち百貨店であるものを、A・Bと仮定する。すると、条件イより、B~Eのうち百貨店であるのは、B・Eとなる。さらに、条件ウより、C~Fのうち百貨店であるのは、Eのみとなる。
ここで、選択肢を確認すると、4・5が該当する。複数の選択肢が該当する場合、同じ条件で、別のパターンを考えてみる。
そこで、条件アより、A~Dのうち百貨店であるものを、B・Cと仮定する。すると、条件イより、B~Eのうち百貨店であるのは、B・Cとなる。さらに、条件ウより、C~Fのうち百貨店であるのは、Cのみとなる。
したがって、業態分類に関して、Eは確実に百貨店であるとはいえない(百貨店でない場合も考えられるから)。
以上より、確実にいえるのは、選択肢5(Fは東京にあるが、百貨店ではない)である。
〔解説〕正答 4
A~Eの発言をまとめると以下のようになる。
| 前半の発言 | 後半の発言 | ※ 「>」は、その人の次に到着 したということを表す(その間に誰かが入るわけではない)。 | |
| A | D>A | E>C | |
| B | E>B | A=5 | |
| C | B>C | D>E | |
| D | D=5 | E>B | |
| E | A>E | C>A |
問題文より、各自の発言(前後半の発言)のうち、一方が正しく、他方はウソということになる。
ここで、B・Dの発言(E>B)に着目する。仮に、この発言をウソとした場合、Bの発言(「A=5」)、Dの発言(「D=5」)が正しくなってしまい、但書の条件に反することになる(同着はいなかった)。
したがって、B・Dの発言(E>B)が正しいことになる。このことから、Aの前半の発言(D>A)が正しく、後半の発言(E>C)が誤りとなる。
そして、Aの前半の発言が正しいことから、Cの後半の発言(D>E)、Eの後半の発言(C>A)が誤りとなる(C・Eの前半の発言が正しいことになる)。
以上より、山頂への到着した順番は、D>A>E>B>Cとなる。
〔解説〕正答 3
選択肢2、3、5に仮定があるので、結論がいえるか確認をしていく。
選択肢2:Bが決勝戦に進んだ場合(Eと決勝で当たる)
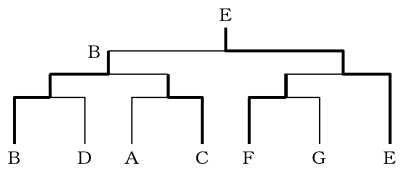
選択肢3:Dが優勝した場合(E、FとDは別ブロックになる)
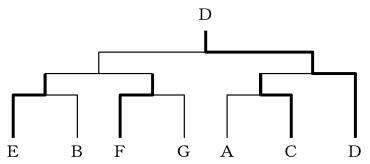
選択肢5:Gが決勝戦に進んだ場合(F、Gは決勝で当たる)
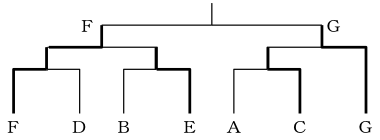
選択肢1、4はいずれのケースでも該当しない。正しくいえるのは選択肢3となる。
〔解説〕正答 5
集合の問題は特定の数字を計算するために、問題を図表に書き込むことが重要です。
集合の図表はいくつかありますが、コの問題の場合、A大学・B大学、正解・不正解の他に、第1問の○×と第2問の○×という場合分けが必要となります。次のような表を書くとわかりやすいでしょう。
問題文を表に記入すると次のようになる。
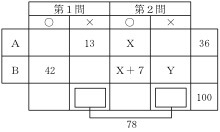
(図1)
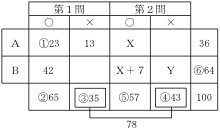
(図2)
①Aの人数は 36人なので、第1問を正解した人数は 23人。
②第一問の正解者は 65人、③全員で 100人なので第1問の不正解は 35人。
④第1問と第2問の不正解の合計は 78人なので第2問の不正解は 43人。
⑤全員が 100人なので、第2問の正解者の合計は 57人となる。
X+ (X+7 )= 78 X= 25
第2問の正解者は 25+ 7= 32名となる。
⑥全員が 100名なのでB大学は 64名となる。
以上より、B大学で第2問を不正解となった者は、 64- 32= 32名となる。
〔解説〕正答 2
A、B、Cの1分間当たりの作業量をそれぞれa、b、cとし、全仕事量をWとすると、問題の条件より次の式が立つ。
25(a+b)=W …… ① 30(b+c)=W …… ② 10(a+b+c)+22b=W …… ③
①式×6、②式×5
25(a+b)×3=W×6 150a+150b=6W …… ④
30(b+c)×5=W×5 150b+150c=5W …… ⑤
③式×15
10(a+b+c)×15+22b×15=W×15
150a+150b+150c+330b=15W
150a+480b+150c=15W …… ⑥
⑥式-④式-⑤式
150a+480b+150c=15W
-)150a+150b = 6W
-) 150b+150c= 5W
─────────────
180b = 4W
∴ 45b=W …… ⑦
bはBの1分当たりの作業量であるから、⑦式の左辺45bはBが45分間作業したことを表す。
また右辺Wは全仕事量であるから、⑦式はBが45分間作業をするとそれは全仕事量となり仕事を仕上げる事ができることを表している。
〔解説〕正答 2
共通する十の位をxとすると、百の位は8-x、一の位は7-xとなるが、この数は3の倍数であるから、この3桁の数を合計すると3の倍数になるはずである。3つの桁を合計すると、
x+(8-x)+(7-x)=15-x
となる。
15は3の倍数であるから、xが3の倍数であれば、この数は3の倍数となる。
よって、xが3、6、9の3通りが3の倍数となるので、3個。
〔解説〕正答 5
全員から3人を選ぶ組合せは、10C3=10×9×8/3×2×1 =120通り
女性の姉妹をA、B、親族関係の女性をC、D、その他の一人をEとすると、女性3人を選んだとき、2人が親族関係になる場合はAB、CDの2通り。
残りの1人はEを含む3人となるので、6通り。
女性2人を選んだ場合、親族関係になるケースは、AB、CDの2通り
残りの男性1人は5通りなので、2×5=10通り
男性のみ3人選んだ場合は 5C3=5×4×3/3×2×1 =10通り
したがって、チームの組合せは、120-(6+10+10)=94通りとなる。
〔解説〕正答 3
素数とは1以外でその数でしか割れない数をいう。
2つのサイコロの和は最大で8+8=16となるが、1~16までの中で素数は、2、3、5、7、11、13の6個である。
(1,1)(1,2)(1,4)(1,6)
(2,3)(2,5)
(3,4)
(3,8)
(4,7)
(5,6)(5,8)
(6,7)
(1,1)を除く11ケースは1個目に出る場合と2個目に出る場合の2通りがあるので合計23通り。サイコロを2個の場合の下図は8×8=64通りとなる。
したがって、確率は23/64となる。
〔解説〕正答 4
ショートケーキの個数をX個、価格をY円とする。チョコレートケーキの個数は(40-X)個、価格は(Y-150)円または(Y+150)円となる。
ショートケーキがチョコレートケーキよりも150円高い場合を想定する。
X×Y+(40-X)÷2×(Y-150)+(40-X)÷2×(Y-180)=X×Y+(40-X)×(Y-150)-480
(40-X)÷2×(Y-180)=(40-X)÷2×(Y-150)-480
(40-X)÷2×(-30)=-480
-600+15X=-480
15X=120
X=8
8×Y×2=16×(Y-180)+16×(Y-150)
16Y=32Y-5280
Y=330
〔解説〕正答 3
問題の状況を表すと次のようになる。
1,3,○,○,○,a
1,3,○,○,○,a,3a
3倍して約数が一つ増えるということは最初の2桁に3の約数があることになる。(3がなければ3と3倍した数の最低2個は増えることになるため)
選択肢の数字になる場合を考える。
4→14か41だが、3の倍数ではないので該当しない。
6→23、32、16,61だが、すべて3の倍数でないため該当しない。
8→24、42,18,81となる。
24の場合、1,2,3,4,6,8,12,24と8個。
42の場合、1,2,3,6,7,21,42と7個。
18の場合、1,2,3,6,9,18と6個
81の場合、1,3,9,27,81の5個となる。
3倍すると243が加わり合計6個となる。
したがって、2桁の数は81となり、10の位と1の位の積は8となる。
この時点で、正答は3となる。
9→33、19、91となる。
33の場合1,3,11,33の4個。
19,91は3の倍数ではない。
12→34、43、26、62が該当する。
すべて3の倍数ではないため該当しない。
〔解説〕正答 2
「2回じゃんけんを行って、初めて勝者が2人決まる」ということは 1回目は同じ種類を全員出したか、全員違う種類を出したことになり決着つかず、2回目で一人が負けたことになる。
グー、チョキ、パーのいずれかで同じになる確率はそれぞれ1/27(=1/3×1/3×1/3)。 グー、チョキ、パー3種類あるので、1/27×3=3/27
全員が違う種類を出す確率を求める。出し方は、1つにつき1/3×1/3×1/3=1/27 3人がそれぞれ違う種類を出す場合の数は3×2=6通り したがって全員が違う種類を出す確率は1/27×6=6/27
1回目 全員同じまたは全員違う確率は3/27+6/27=9/27=1/3
2回目 一人負ける場合、じゃんけんの出し方は一つにつき1/3×1/3×1/3=1/27。
じゃんけんは3種類あるので×3、3人の誰かが負けるので×3、となり1/27×3×3=9/27=1/3
「3回目で1人の勝者が決まる」ということは2回目で勝った2人で3回目を行った結果1人が勝ったことになる。
3回目 1/3×1/3×3×2=6/9=2/3
したがって、「2回じゃんけんを行って、初めて勝者が2人決まり、3回目で1人の勝者が決まる確率」は、
1/3×1/3×2/3=2/27
