昿弌栤戣偺夝朄僙儈僫乕丗敾抐悇棟
崱夞偼曽埵丒埵抲偱偡丅
丂丂乵栤戣乶
丂丂丂丂丂俙乣俧偺俈恖偑師偺傛偆偵侾楍偵暲傫偱偄傞彜揦奨偵弌偐偗丄偦傟偧傟偑暿乆偺揦偵擖
丂丂丂丂偭偨丅埲壓偺傛偆側偙偲偑傢偐偭偰偄傞偲偒丄俙乣俧偺擖偭偨揦偑偡傋偰妋掕偡傞偨傔偵
丂丂丂丂偼偝傜偵偳偺忦審偑昁梫偐丅乮暯惉俈擭崙壠II庬帋尡乯
丂丂丂丂傾丗俙偲俛偑偦傟偧傟擖偭偨揦偺娫偵偼侾尙偺揦偑偁傞丅
丂丂丂丂僀丗俙偼俠傛傝傕丄俤偼俙傛傝傕丄偦傟偧傟岎斣婑傝偺揦偵擖偭偨丅
丂丂丂丂僂丗俥偲俧偑偦傟偧傟擖偭偨揦偺娫偵偼係尙偺揦偑偁傞丅
丂丂丂丂僄丗俧偼俢偺擖偭偨揦偺偡偖椬偱岎斣婑傝偺揦偵擖偭偨丅
 丂丂丂丂1丂俙偼敧昐壆偵擖偭偨丅
丂丂丂丂1丂俙偼敧昐壆偵擖偭偨丅
丂丂丂丂2丂俛偼嫑壆偵擖偭偨丅
丂丂丂丂3丂俠偼掁嬶壆偵擖偭偨丅
丂丂丂丂4丂俢偼庰壆偵擖偭偨丅
丂丂丂丂5丂俥偼梞暈壆偵擖偭偨丅
丂丂丂丂
丂丂丂丂丂惓摎丂俀
丂丂丂丂丂曽埵丒埵抲偵娭偡傞弌戣偱偁傞丅崙壠II庬帋尡偵偍偄偰偼丄偙偺暘栰偺弌戣偑懡偄偺偱
丂丂丂丂廫暘側栤戣墘廗偑昁梫偲巚傢傟傞丅
丂丂丂丂丂傑偢傾偐傜僄偺忦審傪恾帵偟丄偦傟傜傪柕弬偟側偄傛偆偵慻傒崌傢偣偰偄偔丅偨偩偟丄
丂丂丂丂乽柕弬偟側偄傛偆偵乿偲偄偭偰傕丄峫偊側偑傜慻傒崌傢偣偰偄偔偺偼擄偟偄偺偱丄慻傒崌
丂丂丂丂傢偣偨屻偱丄傕偆堦搙丄慡偰偺忦審偵柕弬偟偰偄側偄偐偳偆偐偺妋擣偑昁梫偱偁傞丅傑偨丄
丂丂丂丂慻傒崌傢偣傞帪偵傕丄敾抐悇棟偺栤戣偱傛偔搊応偡傞乽応崌暘偗乿偺峫偊曽傪梡偄側偑傜
丂丂丂丂慻傒崌傢偣偰偄偔偲惍棟偟傗偡偔側傞丅埲壓丄偙傟傜偺億僀儞僩傪偙偺栤戣傪捠偟偰妋擣
丂丂丂丂偡傞丅
丂丂丂丂侾丏忦審偺傾偐傜僄傑偱傪恾帵偡傞丅
丂丂丂丂乮忦審傾乯
丂丂丂丂丂丂丂丂丂丂俙劅仜劅俛丂丂傕偟偔偼丂丂俛劅仜劅俙
丂丂丂丂丂偙偺傛偆偵丄偳偪傜偑岎斣偵嬤偄偐偑暘偐傜側偄傛偆側応崌偵偼丄俀捠傝偺応崌傪峫偊
丂丂丂丂偰恾帵偡傞丅
丂丂丂丂
丂丂丂丂乮忦審僀乯
丂丂丂丂丂丂丂丂丂丂俤丂劅丂俙丂劅丂俠丂乮偨偩偟丄娫偵扤偐偑偄傞壜擻惈偁傝乯
丂丂丂丂乮忦審僂乯
丂丂丂丂丂俥劅仜劅仜劅仜劅仜劅俧丂傕偟偔偼丂俧劅仜劅仜劅仜劅仜劅俥
丂丂丂丂乮忦審僄乯
丂丂丂丂丂丂丂丂丂丂俧劅俢
丂丂丂丂俀丏恾帵偟偨忦審偺傾偐傜僄傑偱傪慻傒崌傢偣偰偄偔丅
丂丂丂丂丂慻傒崌傢偣傞嵺丄慜弎偟偨傛偆偵乽応崌暘偗乿傪偟側偑傜峫偊傞偲偆傑偔慻傒崌傢偣傞
丂丂丂丂偙偲偑偱偒傞丅偙偺栤戣偱偼丄忦審僂傛傝丄俥偲俧偺娫偺娫妘偑嵟傕嬻偄偰偄傞偺偱丄俥
丂丂丂丂偲俧傪婎弨偵慻傒崌傢偣偰偄偔偺偑傛偄丅傑偨丄慻傒崌傢偣傞応崌丄恖悢傪偒偞傫偩悢捈
丂丂丂丂慄傪傕偲偵慻傒崌傢偣偰偄偔偺傕堦偮偺曽朄偱偁傞丅
丂丂丂丂丂働乕僗侾乮俥偑嵟傕岎斣婑傝偺梞暈壆偵擖偭偨偲壖掕偟偨応崌乯
丂丂丂丂丂俥丒俧丒俢偺埵抲偼偡偖偵妋掕偡傞偺偱丄拲堄偡傋偒揰偼俙偲俛偺埵抲偳傝偱偁傞丅偙
丂丂丂丂傟傕忦審傾偱恾帵偟偨傛偆偵俀捠傝偁傞偨傔丄俀捠傝偺応崌偵暘偗偰慻崌偣側偗傟偽側傜
丂丂丂丂側偄丅慡偰偺忦審傪慻傒崌傢偣傞偲師偺俀捠傝偺慻崌偣偑峫偊傜傟傞丅
丂丂丂丂丂劙劒劒劥劒劒劥劒劒劥劒劒劥劒劒劥劒劒劜
丂丂丂丂丂俥丂丂俤丂丂俙丂丂俠丂丂俛丂丂俧丂丂俢
丂丂丂丂
丂丂丂丂丂俥丂丂俛丂丂俤丂丂俙丂丂俠丂丂俧丂丂俢
丂丂丂丂
丂丂丂丂丂働乕僗俀乮俥偑暥嬶壆偵擖偭偨偲壖掕偟偨応崌乯
丂丂丂丂丂俥偑嵍偐傜俀斣栚偺暥嬶壆偵擖偭偨偲壖掕偡傞偲丄堦斣塃抂偺庰壆偵俧偑擖偭偨偙偲偵
丂丂丂丂側傞丅偟偐偟丄忦審僄傛傝丄俧偺擖偭偨塃椬偺揦偵俢偑擖傜側偗傟偽側傜偢丄庰壆偺塃椬
丂丂丂丂偵揦偼側偄偺偱偙偺働乕僗偼峫偊傜傟側偄偙偲偵側傞丅
丂丂丂丂丂埲忋偑俥偑俧傛傝傕岎斣婑傝偺揦偵擖偭偨偲壖掕偟偨応崌偺慻崌偣偱偁傞丅師偵俧偑俥
丂丂丂丂傛傝岎斣婑傝偺揦偵擖偭偨応崌傪応崌暘偗偟側偑傜峫偊偰傒傞丅
丂丂丂丂
丂丂丂丂丂働乕僗俁乮俧偑嵟傕岎斣婑傝偺梞暈壆偵擖偭偨偲壖掕偟偨応崌乯
丂丂丂丂丂俧丒俢丒俥偺埵抲偼偡偖偵妋掕偡傞偺偱丄偙偺応崌偵傕拲堄偡傋偒揰偼俙偲俛偺埵抲偳
丂丂丂丂傝偱偁傞丅偙傟傕忦審傾偱恾帵偟偨傛偆偵俀捠傝峫偊傜傟傞偑丄忦審僀偺俤亅俙亅俠偺暲
丂丂丂丂傃傪峫偊傞偲俙偑俛傛傝嵍懁偺揦偵偄傞偙偲偼偁傝摼側偄偺偱師偺慻崌偣偩偗偲側傞丅
丂丂丂丂丂劙劒劒劥劒劒劥劒劒劥劒劒劥劒劒劥劒劒劜
丂丂丂丂丂俧丂丂俢丂丂俛丂丂俤丂丂俙丂丂俥丂丂俠
丂丂丂丂
丂丂丂丂丂働乕僗係乮俧偑暥嬶壆偵擖偭偨偲壖掕偟偨応崌乯
丂丂丂丂丂働乕僗俀偲摨條偵丄俧偑暥嬶壆偵擖偭偨応崌傪壖掕偟偰傒傞偲丄師偺傛偆側慻崌偣偑偱
丂丂丂丂偒偁偑傞丅
丂丂丂丂丂劙劒劒劥劒劒劥劒劒劥劒劒劥劒劒劥劒劒劜
丂丂丂丂丂俤丂丂俧丂丂俢丂丂俙丂丂俠丂丂俛丂丂俥
丂丂丂丂丂埲忋偺偙偲偐傜丄忦審傾偐傜僄傑偱傪傕偲偵峫偊傜傟傞俈恖偺擖偭偨揦偺壜擻惈偼係捠
丂丂丂丂傝偁傞偙偲偑暘偐傞丅
丂丂丂丂丂劙劒劒劥劒劒劥劒劒劥劒劒劥劒劒劥劒劒劜
丂丂丂丂丂俥丂丂俤丂丂俙丂丂俠丂丂俛丂丂俧丂丂俢丂乧乧丂僀
丂丂丂丂
丂丂丂丂丂俥丂丂俛丂丂俤丂丂俙丂丂俠丂丂俧丂丂俢丂乧乧丂儘
丂丂丂丂
丂丂丂丂丂俧丂丂俢丂丂俛丂丂俤丂丂俙丂丂俥丂丂俠丂乧乧丂僴
丂丂丂丂
丂丂丂丂丂俤丂丂俧丂丂俢丂丂俙丂丂俠丂丂俛丂丂俥丂乧乧丂僯
丂丂丂丂丂偙偺栤戣偱偼丄乽俙偐傜俧偺擖偭偨揦偑偡傋偰妋掕偡傞偨傔偺忦審乿傪慖傇偺偱偁傞偐
丂丂丂丂傜丄慖戰巿侾偐傜慖戰巿俆傑偱偺忦審傪捛壛偟偰丄係捠傝偁傞壜擻惈偐傜侾捠傝偵偟傏傞
丂丂丂丂偙偲偑偱偒傞傕偺偑惓摎偲側傞丅
丂丂丂丂丂慖戰巿侾傪忦審偲偟偰捛壛偡傞偲丄係捠傝偺偆偪偺儘傑偨偼僯偺俀捠傝偺応崌偵偼偟傏
丂丂丂丂傞偙偲偑偱偒傞偑丄侾捠傝乮尵偄姺偊傞偲丄俙偐傜俧偺擖偭偨揦偑偡傋偰妋掕偡傞乯偵偼
丂丂丂丂妋掕偟側偄偺偱惓摎偲偼側傜側偄丅
丂丂丂丂丂慖戰巿俀傪捛壛偡傞偲丄係捠傝偺偆偪偺僴偺応崌偵尷掕偝傟傞偺偱丄惓摎偼慖戰巿俀偲
丂丂丂丂側傞丅
丂丂丂丂丂側偍丄慖戰巿俁傪捛壛偡傞偲儘傑偨偼僯偺俀捠傝丄慖戰巿係傪捛壛偡傞偲僀傑偨偼儘偺
丂丂丂丂俀捠傝丄慖戰巿俆傪捛壛偡傞偲僀傑偨偼儘偺俀捠傝偺応崌偑峫偊傜傟偰偟傑偆偨傔偵丄偡
丂丂丂丂傋偰傪妋掕偡傞偙偲偼偱偒偢丄惓摎偲偼側傜側偄丅
丂丂丂丂
丂丂儂乕儉儁乕僕傊栠傞乧丂丂丂昿弌栤戣偺夝朄僙儈僫乕乧
戞俆夞偼埵抲偺栤戣偱偡丅
昁偢恾帵偟偰峫偊傑偟傚偆丅
丂丂
丂丂丂乵栤戣乶俙乣俥偺俇恖偼偦傟偧傟偺帺戭偺埵抲娭學偵偮偄偰師偺傛偆偵弎傋偨偑丄偙傟傜偺
丂丂丂丂敪尵偐傜妋幚偵偄偊傞偺偼偳傟偐丅乮暯惉俇擭崙壠II庬帋尡乯
丂丂丂丂丂俙丗巹偺壠偐傜900倣恀杒偵俥偺壠偑偁傞丅
丂丂丂丂丂俛丗俙偺壠偼巹偺壠偺撿惣偵偁傝丄俢偺壠偼巹偺壠偵嵟傕嬤偄丅
丂丂丂丂丂俠丗巹偺壠偼俛偺壠偺杒搶偵偁傞丅
丂丂丂丂丂俢丗巹偺壠偼俥偺壠偺恀搶偵丄俤偺壠偺恀惣偵偁傞丅
丂丂丂丂丂俤丗巹偺壠偼俠偺壠偐傜450倣恀撿偵偁傞丅
丂丂丂丂丂俥丗巹偺壠偼俛偺壠偺杒惣偵偁傞丅
丂丂丂丂1丂俙偺壠偐傜俠偺壠傑偱偺嫍棧偼1350倣偱偁傞丅
丂丂丂丂2丂俛偺壠偼丄俙丄俤丄俥偺偦傟偧傟偺壠偐傜摍嫍棧偵偁傞丅
丂丂丂丂3丂俠偺壠偐傜俢偺壠傑偱偺嫍棧偲丄俛偺壠偐傜俤偺壠傑偱偺嫍棧偼摨偠偱偁傞丅
丂丂丂丂4丂俢偺壠偼丄俛偺壠偺恀杒偵偁傞丅
丂丂丂丂5丂俤偺壠偐傜俥偺壠傑偱偺嫍棧偼丄俠偺壠偐傜俤偺壠傑偱偺嫍棧偺俁攞偱偁傞丅
丂丂丂丂
丂丂丂丂乵惓摎丂俆乶
丂丂丂丂丂曽埵丒埵抲偵娭偡傞栤戣偱偁傞丅偙偺栤戣偼丄忦審傪傒傞偲丄俙乣俥偺埵抲娭學偑曽埵
丂丂丂丂傪婎弨偲偟偰弎傋傜傟偰偄傞偺偱丄曽埵偑娭學偟偰偄傞壠偺弴彉傪傕偲偵偟偰曽妏傪娫堘
丂丂丂丂偊側偄傛偆偵恾帵偟偰偄偔丅
丂丂丂丂丂傑偨丄偙偺庬椶偺栤戣偱偼丄忦審偵傛偭偰丄曽埵偼忦審偱採帵偝傟偰偄傞偑丄嫍棧偵偮
丂丂丂丂偄偰偼採帵偝傟偰偄側偄応崌傕偁傝丄偦偺傛偆側応崌偵偼奩摉偡傞曽岦偺墑挿慄忋偺偳偙
丂丂丂丂偺晹暘偵傕奩摉偡傞壜擻惈偑偁傞偺偱拲堄偑昁梫偱偁傞丅
丂丂丂丂偙偺栤戣偱偼丄俙仺俢仺俤仺俥丒俛丒俠偺弴彉偱恾帵偟偰偄偔丅
丂丂丂丂丂嫍棧偵偮偄偰拲堄偟側偑傜曽埵傪娫堘偊側偄傛偆偵偟偰丄俙仺俢仺俤仺俥丒俛丒俠偺弴
丂丂丂丂彉偱恾帵偟偰偄偔偲師偺傛偆偵側傞丅
丂丂丂丂丂丂丂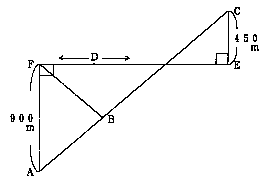 丂丂丂丂
丂丂丂丂
丂丂丂丂丂俠丒俥偺敪尵傪傒傞偲丄慡偰俛偲偺埵抲娭學偵偮偄偰弎傋傜傟偰偄傞偺偱丄偦偙偵拲栚
丂丂丂丂偡傞偲丄慡懱偺埵抲娭學偑恾帵偟傗偡偄偲巚傢傟傞丅傑偨丄暿偺尒曽傪偡傞偲丄偦偺敪尵
丂丂丂丂偐傜丄俛偐傜傒偰俙偼撿惣丄俠偼杒搶偵埵抲偟偰偄傞偺偱丄俙俠偺捈慄忋偵俛偑埵抲偟丄
丂丂丂丂偟偐傕丄俛偐傜傒偰杒惣偵俥偑埵抲偡傞傛偆側揰偵俛偑埵抲偟偰偄傞偙偲偑暘偐傞丅
丂丂丂丂丂傑偨丄偙偺栤戣偱偼丄俢偵偮偄偰偼丄偦傟偧傟曽埵偼忦審偱採帵偝傟偰偄傞偑丄嫍棧偵
丂丂丂丂偮偄偰偼採帵偝傟偰偄側偄偨傔偵丄慜弎偟偨傛偆偵丄奩摉偡傞曽岦偺墑挿慄忋偺偳偙偺晹
丂丂丂丂暘偵傕奩摉偡傞壜擻惈偑偁傞偺偱拲堄偑昁梫偱偁傞丅
丂丂丂丂丂偙傟傜偺揰偵拲堄偟偰丄恾帵偝傟偨慡懱恾傪傒偰傒傞偲丄曗彆慄傪擖傟傞偙偲偱師偺傛
丂丂丂丂偆偵峫偊傞偙偲偑偱偒傞丅
丂丂丂丂丂丂丂丂丂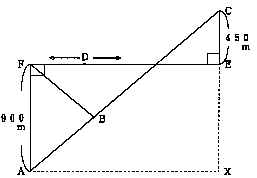 丂
丂
丂丂丂丂丂忋偺恾偵偍偄偰揰慄傪擖傟丄嶰妏宍俙倃俠傪尒偰傒傞偲丄佢俙倃俠偼90亱丄佢倃俙俠媦
丂丂丂丂傃佢倃俠俙偼俛偐傜傒傞偲堦捈慄忋偱偁傝丄撿惣媦傃杒搶偺曽埵側偺偱丄45亱偺妏搙偲側
丂丂丂丂傞丅偟偨偑偭偰丄嶰妏宍俙倃俠偼捈妏擇摍曈嶰妏宍偱偁傝丄曈俙倃亖曈俠倃丄俠倃偺挿偝
丂丂丂丂偼俙俥亄俤俠傛傝丄1350倣偲側傞偙偲偑傢偐傞丅埲忋偺偙偲偐傜慖戰巿傪専摙偟偰傒傞偲
丂丂丂丂慖戰巿侾偼俙俠偺挿偝偼1350亊併2 偲側傞偺偱岆傝偱偁傞丅慖戰巿俀偼俛偺埵抲偐傜俙丒
丂丂丂丂俥偼摍嫍棧偲尵偊傞偑丄俤偲偼摍嫍棧偲偼側傜側偄偺偱岆傝偱偁傞丅傑偨丄慖戰巿俁媦傃
丂丂丂丂慖戰巿係偼俢偵偮偄偰偼俥偲俤傪寢傫偩墑挿慄忋偺偳偙偱傕峫偊傜傟傞偺偱妋幚偵偼偄偊
丂丂丂丂側偄丅慖戰巿俆偼俤乣俥偺嫍棧偼俙倃偺嫍棧偲摍偟偄偺偱1350倣丄俠乣俤偺壠偺嫍棧偼45
丂丂丂丂0倣傛傝丄1350亐450亖俁偲側傞偺偱丄慖戰巿俆偑惓摎偲側傞丅
戞係夞偼弴彉偺栤戣偱偡丅
偙偺庬偺栤戣偼忦審傪恾帵偟偰偄偔偺偑懍偔夝偔僐僣偱偡丅
丂乵栤戣乶偁傞3000倣嫞憟偵俙乣俤偺俆恖偑嶲壛偟偨丅廔斦偵嬤偯偄偨偁傞偲偒丄師偺傛偆側忬嫷
丂丂丂丂偱偁傞偙偲偑傢偐偭偨丅偦偺偲偒偺俆恖偺忬懺偵偮偄偰偺婰弎偲偟偰惓偟偄傕偺偼偳傟偐丅
丂丂丂丂乮暯惉係擭崙壠II庬帋尡乯
丂丂丂丂丂丒愭摢偺慖庤偲嵟屻旜偺慖庤偼14倣棧傟偰偄傞丅
丂丂丂丂丂丒俙慖庤偲俛慖庤偺娫妘偼俉倣偱丄俛慖庤偼俠慖庤傛傝11倣抶傟偰憱偭偰偄傞丅
丂丂丂丂丂丒俢慖庤偼俆恖偺拞偱俁斣栚偺弴埵傪憱偭偰偄偰丄俤慖庤偲偺娫妘偼俈倣偱偁傞丅
丂丂丂丂1丂俙慖庤偲俢慖庤偺娫妘偼係倣偱偁傞丅
丂丂丂丂2丂俛慖庤偲俤慖庤偺娫妘偼俆倣偱偁傞丅
丂丂丂丂3丂俛慖庤偲俢慖庤偺娫妘偼俀倣偱偁傞丅
丂丂丂丂4丂俠慖庤偲俢慖庤偺娫妘偼俇倣偱偁傞丅
丂丂丂丂5丂俢慖庤偼俙慖庤傛傝愭傪憱偭偰偄傞丅
丂丂丂丂
丂丂丂丂丂惓摎丂侾
丂丂丂丂丂弴彉偵娭偡傞弌戣偱偁傞丅弴彉傪寛掕偡傞栤戣偱偼丄悢捈慄傪梡偄偰忦審傪惍棟偡傞偲
丂丂丂丂夝摎偑摼傜傟傗偡偄丅偙偺栤戣偱偼丄俁偮偺忦審傪恾帵偟側偑傜偦傟傜傪悢捈慄忋偱傑偲
丂丂丂丂傔偰偄偔丅
丂丂丂丂丂嵟弶偺忦審偱偼丄愭摢偲嵟屻旜偺娫妘偑14倣偲側偭偰偄傞偺偱悢捈慄偺挿偝偑14倣偲側
丂丂丂丂傞偙偲偑暘偐傝丄偙偺拞偵俆恖偺埵抲傪偲傟傞傛偆偵偡傟偽傛偄丅
丂丂丂丂丂劌劅劅劅劅丂丂丂丂侾係倣丂丂丂劅劅劅劅劅劅劎
丂丂丂丂丂劙劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劜
丂丂丂丂
丂丂丂丂丂俀斣栚偺忦審傪傒傞偲丄俙慖庤偲俛慖庤偺娫妘偑俉倣偲偁傞丅偙偺応崌丄偳偪傜偑慜偱
丂丂丂丂偳偪傜偑屻傠偑暘偐傜側偄偨傔丄偲傝偁偊偢恾帵偡傞偲師偺傛偆偵側傞丅
丂丂丂丂
丂丂丂丂丂劌劅劅丂丂俉丂倣丂丂劅劅劎
丂丂丂丂丂劙劒劒劒劒劒劒劒劒劒劒劒劜
丂丂丂丂丂俙丂丂丂丂丂丂丂丂丂丂丂俛
丂丂丂丂乮俛乯丂丂丂丂丂丂丂丂丂乮俙乯
丂丂丂丂丂偟偐偟丄師偺忦審傪傒傞偲丄俛慖庤偼俠慖庤傛傝11倣抶傟偰憱偭偰偄傞偲偺婰弎偑偁傞
丂丂丂丂偺偱丄傕偟俛慖庤偑俙慖庤偺俉倣慜偵偄傞偲壖掕偡傞偲丄俠慖庤偐傜俙慖庤傑偱偺娫妘偼
丂丂丂丂19倣偲側偭偰偟傑偄丄嵟弶偺忦審偲柕弬偟偰偟傑偆丅傛偭偰俙慖庤偲俛慖庤偺俉倣偺娫妘
丂丂丂丂偼俙慖庤偑俛慖庤偺俉倣慜偵偄傞偙偲偵側傞丅埲忋傪恾帵偡傞偲師偺傛偆偵側傞丅
丂丂丂丂丂劌劅劅劅劅丂侾侾丂倣丂劅劅劅劅劅劅劅劎
丂丂丂丂丂丂丂丂丂丂劌劅劅丂丂俉丂倣丂劅劅劅劅劎
丂丂丂丂丂劙劒劒劒劒劥劒劒劒劒劒劒劒劒劒劒劒劒劜
丂丂丂丂丂俠丂丂丂丂俙丂丂丂丂丂丂丂丂丂丂丂丂俛
丂丂丂丂丂師偵俁斣栚偺忦審傪傒傞偲丄俢慖庤偑俁斣栚偺弴埵傪憱偭偰偄傞偲偁傞偺偱嵟弶偺恾偺
丂丂丂丂俁斣栚偺埵抲偵俢慖庤偑擖傞丅偨偩偟丄俤慖庤偼偦偺慜偐屻傠偐偼暘偐傜側偄丅
丂丂丂丂丂偙傟傜傪柕弬偟側偄傛偆偵侾偮偵傑偲傔偰偄偔偑丄愭摢偲嵟屻旜偺娫妘偑14倣偱偁傞偺
丂丂丂丂偱丄俠慖庤傪愭摢偲偟偨応崌偲俀斣栚偺応崌偺俀捠傝偑峫偊傜傟傞丅
丂丂丂丂乵侾乶丂俠慖庤偑愭摢偺応崌
丂丂丂丂丂俠慖庤偑愭摢偩偲偟偨応崌丄係斣栚偵俛慖庤偲側傝丄俀斣栚偵俙慖庤丄巆偭偨嵟屻旜偵
丂丂丂丂俤慖庤偲側傞丅(俛慖庤傪嵟屻旜偲偡傞偲14倣偺娫妘偑11倣偲側傝柕弬偡傞)
丂丂丂丂丂劌劅劅劅劅劅劅丂侾係倣丂劅劅劅劅劅劅劅劅劎
丂丂丂丂丂劙劒劒劒劒劥劒劒劒劒劥劒劒劒劒劥劒劒劒劒劜
丂丂丂丂丂俠丂丂丂丂俙丂丂丂丂俢丂丂丂丂俛丂丂丂丂俤
丂丂丂丂丂偙偙偱丄愭摢偺慖庤傪14倣丄嵟屻旜偺慖庤傪侽倣丄俢慖庤傪俈倣偺埵抲偲偟偰奺慖庤偺
丂丂丂丂娫妘傪寁嶼偟偰偄偔丅
丂丂丂丂丂俠慖庤偲俛慖庤偺娫妘偼11倣側偺偱丄俛慖庤偼俤慖庤偺俁倣愭丄俙慖庤偼俛慖庤偺俉倣
丂丂丂丂愭側偺偱丄俤慖庤偐傜11倣愭偵埵抲偟偰偄傞偙偲偵側傝丄奺恖偺娫妘偼師偺恾偺乮丂乯悢
丂丂丂丂丂帤偺傛偆偵側傝丄慡懱偺弴彉偑柕弬側偔惉棫偡傞丅
丂丂丂丂丂劌劅劅劅劅劅劅丂侾係倣丂劅劅劅劅劅劅劅劅劎
丂丂丂丂丂劙劒劒劒劒劥劒劒劒劒劥劒劒劒劒劥劒劒劒劒劜
丂丂丂丂丂俠丂丂丂丂俙丂丂丂丂俢丂丂丂丂俛丂丂丂丂俤
丂丂丂丂丂14乮俁乯丂11乮係乯丂俈乮係乯丂俁乮俁乯丂侽
丂丂丂丂丂乵俀乶丂俠慖庤偑俀斣栚偺埵抲偺応崌
丂丂丂丂丂俠慖庤傪俀斣栚偲偡傞偲丄俙慖庤偑係斣栚丄俛慖庤偑俆斣栚偲側傝丄愭摢偼巆偭偨俤慖
丂丂丂丂庤偲側傝師偺傛偆側弴彉偲側傞丅
丂丂丂丂丂劌劅劅劅劅劅丂丂侾係倣丂丂丂劅劅劅劅劅劅劎
丂丂丂丂
丂丂丂丂丂劙劒劒劒劒劥劒劒劒劒劥劒劒劒劒劥劒劒劒劒劜
丂丂丂丂丂俤丂丂丂丂俠丂丂丂丂俢丂丂丂丂俙丂丂丂丂俛
丂丂丂丂丂偙偙偱丄奺恖偺娫妘偑柕弬側偔惉棫偡傞偐偳偆偐傪専摙偡傞丅
丂丂丂丂丂俠慖庤偲俛慖庤偺娫妘偼11倣側偺偱丄俠慖庤偼俛慖庤偺11倣愭丄俙慖庤偼俛慖庤偺俉倣
丂丂丂丂愭偱偁傞丅偟偐偟丄俢慖庤偲俤慖庤偺娫妘偼俈倣側偺偱丄俙慖庤偑俛慖庤偺俉倣愭偲側傞
丂丂丂丂偲丄俢慖庤偼係斣栚偲側傞偨傔偵柕弬偟偰偟傑偄丄偙偺弴彉偼惉棫偟側偄偙偲偑暘偐傞丅
丂丂丂丂丂劌劅劅劅劅劅丂丂侾係倣丂丂丂劅劅劅劅劅劅劎
丂丂丂丂
丂丂丂丂丂劙劒劒劒劒劥劒劒劒劒劥劒劒劒劒劥劒劒劒劒劜
丂丂丂丂丂俤丂丂丂丂俠丂丂丂丂俙丂丂丂丂俢丂丂丂丂俛
丂丂丂丂丂14乮俁乯丂11乮係乯丂俉丂丂丂丂俈丂丂丂丂侽
丂丂丂丂丂偟偨偑偭偰丄峫偊傜傟傞偺偼俠偑愭摢偺応崌偩偗偱偁傝丄奺恖偺娫妘傪傕偲偵慖戰巿傪
丂丂丂丂専摙偡傞偲惓摎偼慖戰巿侾偲側傞丅
丂丂丂丂
丂丂丂儂乕儉儁乕僕傊栠傞乧丂丂丂昿弌栤戣偺夝朄僙儈僫乕乧
丂丂丂丂丂戞俁夞栤戣
乵栤戣乶偁傞抮偱峴傢傟偨掁傝戝夛偵俙乣俥偺俇恖偑嶲壛偟偨丅嶲壛幰偺埵抲偵偮偄偰俙乣俥偺俆恖偐傜師偺傛偆側敪尵傪摼偨偑丄偙偺偆偪侾恖偩偗偑偆偦傪偮偄偰偄傞偙偲偑暘偐偭偨偆偦傪偮偄偰偄傞偺偼偩傟偐丅側偍丄抮偲嶲壛幰偺娭學偼恾偺傛偆偵側偭偰偄偨丅乮暯惉俇擭丂崙壠II庬乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劇劅劅劅劅劅劅劅劉丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜劆丂丂丂丂丂丂丂劆丂仜
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜劆丂丂丂抮丂丂丂劆丂仜
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜劆丂丂丂丂丂丂丂劆丂仜
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劆丂丂丂丂丂丂丂劆丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂劋劅劅劅劅劅劅劅劊丂丂丂丂丂丂丂丂丂
丂丂丂丂俙丗巹偐傜尒偰惓柺偺塃椬傝偵俢偑嵗偭偰偄偨丅
丂丂丂丂俛丗俠偲俥偼摨偠懁偵嵗偭偰偄偨丅
丂丂丂丂俠丗巹偺惓柺偵偼俛偑嵗偭偰偄偨丅
丂丂丂丂俢丗巹偐傜尒偰惓柺偺侾恖抲偄偨塃椬傝偵俥偑嵗偭偰偄偨丅
丂丂丂丂俤丗巹偐傜尒偰惓柺偺嵍椬傝偵俙偑嵗偭偰偄偨丅
丂丂丂丂侾丂俙
丂丂丂丂俀丂俛
丂丂丂丂俁丂俠
丂丂丂丂係丂俢
丂丂丂丂俆丂俤
丂丂丂丂
丂惓摎丂俁
丂偙偺夁嫀栤戣偼乽曽埵丒埵抲乿偺栤戣偱偁傞丅乽曽埵丒埵抲乿偵娭偡傞栤戣偵偼師偺傛偆側庬椶偺栤戣偑奩摉偡傞丅
丂丂丂乮侾乯丂曽妏丒曽埵偵娭偡傞忦審偐傜埵抲娭學傪専摙偡傞栤戣
丂丂丂乮俀乯丂忦審偐傜丄嵗惾偲拝惾幰傗揦偺攝抲埵抲側偳偺応強傪専摙偡傞栤戣
丂丂丂丂丂偙偺栤戣偼乮俀乯偺庬椶偵奩摉偡傞丅
丂乮俀乯偺庬椶偺栤戣偱偼丄傑偢奺忦審傪恾偱昞偟丄嫟捠偡傞傕偺丄暋悢搊応偡傞傕偺傪拞怱偵慻傒崌傢偣偰偄偔丅偙偺応崌丄慡懱偺攝抲偑恾偱帵偝傟偰偄傞帪偵偼丄慡懱偺攝抲偵摿挜偑側偄偐傪傑偢妋擣偟偰偍偔丅偙偺栤戣偱偼丄抮傪偼偝傫偱嵍塃偵俁儢強偢偮偺埵抲娭學偱偁傞偑丄摿偵恾帵偟偨忦審傪慻傒崌傢偣傞嵺偺摿挜偱偼側偄丅
丂傑偨丄偙偺夁嫀栤戣偱偼丄嶲壛幰偺埵抲娭學偵偮偄偰偺敪尵偺拞偵傂偲偮偩偗偆偦偑偁傞偲偄偆忦審側偺偱丄恾帵偟偨忦審傪慻傒崌傢偣傞嵺偵丄侾偮偺敪尵傪偆偦偲壖掕偟偰(侾偮偺忦審傪彍偄偰懠偺忦審偩偗偱慻傒崌傢偣偰)俇恖偺埵抲偑妋掕偡傞偐偳偆偐傪専摙偡傞昁梫偑偁傞丅
丂丂奺忦審傪恾偱昞偡偲偦傟偧傟師偺傛偆偵側傞丅
丂丂丂丂俙丗俙亅仜丂丂丂俛丗俠丂丂丂丂俠丗俠亅俛丂丂俢丗俥丂丂丂俤丗仜亅俤
丂丂丂丂丂丂丂丂乥丂丂丂丂丂乥喫俛丂丂丂丂丂丂丂丂丂丂丂乥丂丂丂丂丂乥
丂丂丂丂丂丂丂丂俢丂丂丂丂丂俥丂丂丂丂丂丂丂丂丂丂丂丂丂仜丂丂丂丂丂俙
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乥
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仜亅俢
丂忋偺忦審傪慻傒崌傢偣偰偄偔偑丄慜弎偺傛偆偵敪尵偺拞偵偼侾偮偩偗偆偦偑偁傞偺偱丄慻傒崌傢偣傞嵺偵丄俙乣俤偺侾偮傪彍偄偨懠偺係偮偺忦審偱慡偰偺嶲壛幰偺埵抲偑妋掕偡傞偐偳偆偐傪専摙偟偰偄偔丅偙偺偲偒丄傕偟妋掕偡傞偙偲偑偱偒側偗傟偽丄媡偵彍偄偨侾偮偺敪尵偼昁偢杮摉偱偁傞偲暘偐傞丅
丂丂丂丂乮侾乯丂俙偺敪尵偑偆偦偲偟偨応崌
丂丂丂丂丂劇劅劅劅劍劅劅劅劉丂丂丂丂丂丂丂丂
丂丂丂丂丂劆丂俥丂劆丂俤丂劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆丂俠丂劆丂俛丂劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆丂俙丂劆丂俢丂劆丂
丂丂丂丂丂劋劅劅劅劏劅劅劅劊丂丂丂丂丂丂丂丂丂
丂俤偺敪尵撪梕偲柕弬偡傞偙偲偲側傞偺偱丄俙偺敪尵偼杮摉偱偁傞偲暘偐傞丅
丂丂丂丂乮俀乯丂俛偺敪尵偑偆偦偲偟偨応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂劇劅劅劅劍劅劅劅劉丂丂丂丂丂丂丂丂
丂丂丂丂丂劆丂俥丂劆丂俤丂劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆丂俙丂劆丂丂丂劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆丂丂丂劆丂俢丂劆丂
丂丂丂丂丂劋劅劅劅劏劅劅劅劊丂丂丂丂丂丂丂丂丂
丂俠偺敪尵撪梕偲柕弬偡傞偙偲偲側傞偺偱丄俛偺敪尵偼杮摉偱偁傞偲暘偐傞丅
丂丂丂丂乮俁乯丂俠偺敪尵偑偆偦偲偟偨応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂劇劅劅劅劍劅劅劅劉丂丂丂丂丂丂丂丂
丂丂丂丂丂劆丂俥丂劆丂俤丂劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆丂俙丂劆乮俛乯劆丂
丂丂丂丂丂劌劅劅劅劑劅劅劅劎丂丂丂丂丂丂
丂丂丂丂丂劆乮俠乯劆丂俢丂劆丂
丂丂丂丂丂劋劅劅劅劏劅劅劅劊丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂俙丒俛丒俢丒俤丒俥偺敪尵偵偟偨偑偭偰慡堳偺埵抲偑妋掕偡傞偺偱丄俠偑偆偦傪偮偄偰偄傞偙偲偑敾柧偡傞丅
丂丂丂丂
丂丂丂儂乕儉儁乕僕傊栠傞乧丂丂丂昿弌栤戣偺夝朄僙儈僫乕乧
戞俀夞丂栤戣
丂丂丂丂
乵栤戣乶
丂師偺俙乣俠偺慜採忦審偐傜榑棟揑偵偄偊傞傕偺偼丆傾乣僂偺偆偪偳傟偐丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂俙丏塸岅傪榖偝側偄恖偼僼儔儞僗岅傪榖偡丅
丂丂丂丂俛丏僼儔儞僗岅傪榖偝側偄恖偼僗儁僀儞岅傪榖偡丅
丂丂丂丂俠丏僪僀僣岅傪榖偡恖偼僼儔儞僗岅傪榖偝側偄丅
丂丂丂丂傾丏僗儁僀儞岅傪榖偡恖偼塸岅傪榖偡丅
丂丂丂丂僀丏僪僀僣岅傪榖偡恖偼僗儁僀儞岅傪榖偡丅
丂丂丂丂僂丏塸岅傪榖偝側偄恖偼僪僀僣岅傪榖偝側偄丅
丂丂丂丂1丂僀偺傒
丂丂丂丂2丂僂偺傒
丂丂丂丂3丂傾偲僀
丂丂丂丂4丂僀偲僂
丂丂丂丂5丂傾偲僂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俆擭崙壠II庬乯
丂丂丂丂
乵惓摎丂係乶
丂乽榑棟妛揑栤戣乿偲偄偆弌戣暘栰偺栤戣偱偁傞丅乽榑棟妛揑栤戣乿偺婎杮揑側夝朄偲偟偰偼丄
丂丂丂丂丂乮1乯丂婰崋壔偲嶰抜榑朄
丂丂丂丂丂乮2乯丂儀儞恾偵傛傞昞帵
偺俀捠傝偑偁偘傜傟傞丅
丂偙偺栤戣偼乽榑棟妛揑栤戣乿偺拞偱傕婎杮揑側栤戣偱偁傞偺偱丄乮1乯偺婰崋壔偲嶰抜榑朄傪梡偄偨夝朄偱娙扨偵夝偔偙偲偑偱偒傞丅
丂傑偢丄乽榑棟妛揑栤戣乿偺婎杮揑側峫偊曽傪傒偰傒傛偆丅堦斒偵乽榑棟妛揑栤戣乿偵偍偄偰丄乽仜側傜偽仩偱偁傞丅乿偲偄偆傛偆側昞尰傪柦戣偲偄偄丄仜仺仩偲彂偔丅偙傟傪婰崋壔偲偄偄丄偙傟偑惓偟偄応崌偼恀(偟傫)偱偁傞偲偄偄丄岆偭偰偄傞応崌偼婾(偓乯偱偁傞偲偄偆丅
丂傑偨丄仜仺仩偑恀偱偁傞偲偒丄仩偱側偄仺仜偱側偄偲偄偆柦戣傕恀偲側傝丄偙傟傪懳嬼偲偄偄丂
丂丂丂丂丂丂丵丂丵
丂丂丂丂丂丂仩仺仜偲彂偔丅丂丂
丂丂丂丂丂
丂師偵丄壓偺傛偆側俀偮偺柦戣偑偁傞応崌丄
丂丂丂丂丂俙側傜偽俛偱偁傞丅丂丂丂丂丂丂俙仺俛
丂丂丂丂丂俛側傜偽俠偱偁傞丅丂丂丂丂丂丂俛仺俠
丂俙偲俠傪寢傇俛偑偁傞偙偲偐傜丄師偺傛偆偵偄偊傞丅
丂丂丂丂丂備偊偵丄俙側傜偽俠偱偁傞丅丂丂俙仺俠
丂偙偺傛偆側柦戣偺榑棟揑摫偒曽偼嶰抜榑朄偲傛偽傟傞丅
偙傟傜傪慻傒崌傢偣偨傕偺偑丄乽榑棟妛揑栤戣乿偺婰崋壔偲嶰抜榑朄偵傛傞夝朄偱偁傝丄傑偲傔傞偲師偺傛偆偵側傞丅
丂乮侾乯丂栤戣偺忦審偵彂偐傟偨柦戣傪婰崋壔偟偰昞偡丅
丂乮俀乯丂栤戣偺忦審偵彂偐傟偨柦戣偺懳嬼傪婰崋壔偟偰昞偡丅
丂乮俁乯丂奺慖戰巿偺撪梕偑乮侾乯媦傃乮俀乯偺慡偰偺婰崋壔偟偨傕偺傪寢崌偝偣傞偙偲偱尵偊傞偐偳偆偐傪専摙偟夝摎偡傞丅
丂丂丂丂丂栤戣傪忋婰偺乮侾乯乣乮俀乯偺弴彉偱峫偊傞偲師偺傛偆偵側傞丅
丂乮侾乯丂栤戣偺忦審偵彂偐傟偨柦戣傪婰崋壔偟偰昞偡丅
丂丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丂丂丂丵
丂丂丂丂丂丂丂俙丏丂塸仺僼丂丂丂丂俛丏丂僼仺僗丂丂丂俠丏丂僪仺僼
丂乮俀乯丂栤戣偺忦審偵彂偐傟偨柦戣偺懳嬼傪婰崋壔偟偰昞偡丅
丂丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丂丂丂丵
丂丂丂丂丂丂丂俙乫丂僼仺塸丂丂丂丂俛乫丂僗仺僼丂丂丂俠乫丂僼仺僪
丂丂丂丂丂丂丂
丂乮俁乯丂慖戰巿(偙偺栤戣偱偼傾乣僂)偵側傞偐偳偆偐傪乮侾乯丒乮俀乯偺柦戣傪寢崌
丂丂丂丂偝偣専摙偡傞丅
丂丂丂傾丂僗儁僀儞岅傪榖偡恖偼塸岅傪榖偡丅
丂丂丂丂俇偮偺柦戣偺拞偵丄僗偐傜巒傑傞傕偺偼側偄偨傔偵傾偼榑棟揑偵偼尵偊側偄丅
丂丂丂僀丂僪僀僣岅傪榖偡恖偼僗儁僀儞岅傪榖偡丅
丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丵
丂丂丂丂俠傛傝僪仺僼丂俛偵寢崌偟丂僼仺僗丂亪僪仺僗偲偮側偑傞丅
丂丂丂丂丂丂僂丂塸岅傪榖偝側偄恖偼僪僀僣岅傪榖偝側偄丅
丂丂丂丂丂丂丂丂丂丂丂丵丂丂丂丂丂丂丂丂丂丂丂丂丂丵丂丂丂丂丵丂丵
丂丂丂丂丂丂丂俙傛傝丂塸仺僼丂俠乫偵寢崌偟丂丂僼仺僪丂丂丂亪塸仺僪偲偮側偑傞丅
丂埲忋偺偙偲偐傜榑棟揑偵偄偊傞傕偺偼僀媦傃僂偲側傝丄惓摎偼慖戰巿係偲側傞丅
丂戞侾夞栤戣
丂丂丂丂丂丂丂
乵栤戣乶偁傞彫妛峑偺摨妛擭偵俙乣俥偺俇恖偺揮峑惗偑偁傝丄侾慻丄俀慻丄俁慻偺偄偢傟偐偺僋儔僗偵揮擖偝偣傜傟偨丅偦偺忬嫷偑師偺傾乣僆偺傛偆偵傢偐偭偰偄傞偲偒丄妋幚偵偄偊傞偺偼偳傟偐丅
傾丏俇恖偺帣摱偺嫃廧抧嬫偼搶挰侾恖丄惣挰俀恖丄撿挰俁恖偱偁傞丅
僀丏俛偺嫃廧抧嬫偼惣挰偱偁傞偑丄俤偺嫃廧抧嬫偼搶挰偱偼側偔丄俥偺嫃廧抧嬫偼撿挰偱偼側偄丅
僂丏惣挰嫃廧偺帣摱偼堎側傞僋儔僗偵丄傑偨撿挰嫃廧偺帣摱偼奺僋儔僗偵侾恖偢偮揮擖偟偨丅
僄丏俇恖偺偆偪俤偲俠傪娷傓俁恖偑抝巕偱偁傝丄惣挰嫃廧偲撿挰嫃廧偺帣摱偺偆偪丄偦傟偧傟侾恖偩偗偑抝巕偱偁傞丅
僆丏俀慻偵偼俠偩偗丄俁慻偵偼俢偲俤偩偗偑揮擖偟偨丅
侾丏俙偼搶挰嫃廧偺彈巕偱侾慻偵揮擖偟偨丅
俀丏俛偼惣挰嫃廧偺抝巕偱侾慻偵揮擖偟偨丅
俁丏俢偼惣挰嫃廧偺彈巕偱俁慻偵揮擖偟偨丅
係丏俤偼撿挰嫃廧偺抝巕偱俁慻偵揮擖偟偨丅
俆丏俥偼搶挰嫃廧偺抝巕偱侾慻偵揮擖偟偨丅
丂惓摎丂俆
丂敾抐悇棟偺拞偱傕乽懳墳娭學乿偲傛偽傟傞昿弌崁栚偺栤戣偱偁傞丅偙偺庬椶偺栤戣偱偼奺忦審傪昞偵婰擖偟側偑傜丄忦審偐傜敾抐偱偒傞偙偲傪婰擖偟偨傝丄応崌暘偗傪峴側偆偙偲偱惓摎傪尒偮偗偰偄偔丅
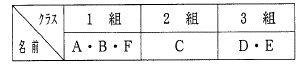
丂偙偺栤戣偱偼丄僆偺忦審偐傜俇恖偲偦偺僋儔僗偺娭學偑師偺傛偆偵寛掕偡傞丅(昞侾)
 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂昞侾丂丂丂丂
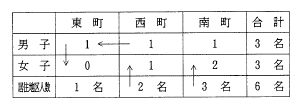
丂傑偨丄忦審傾媦傃僄偐傜丄嫃廧抧嬫偲惈暿偺恖悢娭學偑師偺傛偆偵寛掕偡傞丅(昞俀)
 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂昞俀
丂丂丂丂
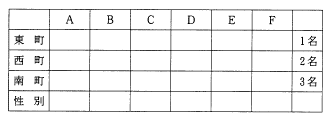
丂師偵丄奺恖偺嫃廧抧嬫傪妋掕偟丄惓摎傪摫偔偨傔偵丄抧嬫偲奺恖偺娭學傪昞宍幃偵偟偰忦審傪婰擖偟偰偄偔丅昞傪嶌惉偡傞偲師偺傛偆側宍偲側傞丅(昞俁)
 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂昞俁
丂丂丂丂丂丂丂丂
丂側偍丄昞傪嶌惉偟偰忦審傪婰擖偟偨傝娭學傪専摙偡傞応崌偵丄捈愙娭學偺側偄忦審傗帒椏(偙偺栤戣偱偼惈暿傗奺挰偺嫃廧恖悢側偳)側偳傕昞偺壓傗嵍塃偵榞傪晅偗懌偡宍偱婰擖偟偰偍偔偲柕弬側偔夝摎偑摫偔偙偲偑偱偒傞偺偱曋棙偱偁傞丅
丂昞傪嶌惉偟偨傜傑偢忦審傪婰擖偡傞丅偙偺帪丄婰擖偼扨偵仜傗亊偺宍偱婰擖偡傟偽傛偄丅
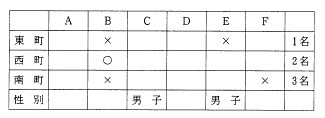
丂傑偢丄忦審偺僀偲僄偑婰擖偱偒傞偺偱師偺傛偆偵婰擖偡傞丅(昞係)
 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂昞係丂丂丂丂
丂婰擖偺嵺丄忦審偐傜敾抐偱偒傞偙偲傕婰擖偡傞丅偙偺栤戣偱偼丄忦審僀傛傝丄俛偑惣挰偲妋掕偟偨偺偱丄俛偺搶挰丒撿挰偼偁傝摼側偄偨傔偵亊偑婰擖偱偒傞丅
師偵懠偺忦審偐傜婰擖偱偒傞晹暘偑側偄偐偳偆偐傪専摙偡傞丅
丂忦審僂傛傝丄撿挰偼奺僋儔僗偵侾柤偢偮偄傞偺偱丄昞侾傛傝丄俀慻偵偄傞俠偼帺摦揑偵撿挰偲側傞丅仺仜媦傃亊傪婰擖(俀慻偼俠侾恖偟偐偄側偄偨傔)
丂忦審僂傛傝丄惣挰嫃廧偺帣摱偼堎側傞僋儔僗偵偄傞偺偱丄俛偑惣挰偲偡傞偲丄俛偲摨偠僋儔僗偺俙丒俥偼惣挰偱偼側偔側傞丅仺亊傪婰擖
丂偙偙傑偱傪婰擖偡傞偲師偺傛偆偵丄俥偺搶挰偲俙偺撿挰偑妋掕偡傞丅(昞俆)
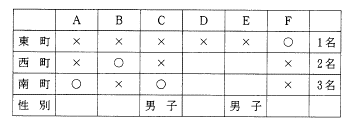
昞俆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
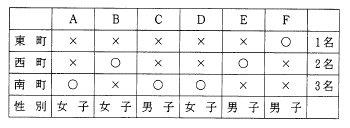
丂嵟屻偵丄昞俀偐傜奺嫃廧抧嬫偵廧傫偱偄傞幰偺惈暿傪妋擣偡傞偲丄搶挰偺侾柤偼抝巕側偺偱丄俥亖抝巕偲側傝丄巆偭偨俙丒俛丒俢偑彈巕偲妋掕偡傞丅偙傟偵傛傝丄惣挰嫃廧偺抝巕偺壜擻惈偑偁傞偺偼俤偩偗側偺偱妋掕偟丄俢偼撿挰偲妋掕丄偟偨偑偭偰惓摎偼慖戰巿俆偲側傞丅(昞俇)
 丂丂丂丂
丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂昞俇
丂丂丂丂
丂丂丂丂
丂丂丂
丂丂丂儂乕儉儁乕僕傊栠傞乧丂丂丂昿弌栤戣偺夝朄僙儈僫乕乧
 丂丂丂丂
丂丂丂丂 丂丂丂丂
丂丂丂丂 丂
丂 丂丂丂丂
丂丂丂丂 丂丂丂丂
丂丂丂丂 丂丂丂丂
丂丂丂丂 丂丂丂丂
丂丂丂丂
 丂丂丂丂
丂丂丂丂