頻出問題の解法セミナー:数的推理
整 数
〔問題 〕A〜Eの5人が100点満点の試験を受けた。5人の得点について次のことがわかっているとき、Eの得点は何点か。ただしA〜Eの得点は全て整数であるとする。
・Aの得点はEの得点の3分の1であった。
・Bの得点はEの得点の5分の1であった。
・Cの得点はEの得点の2分の3であった。
・Dの得点はA〜Cの得点の合計に21点を加えたものの2分の1であった。
1.15点
2.30点
3.45点
4.60点
5.75点
正答 2
整数の性質を解法に用いる問題を整数問題という。この場合、問題の条件より作られる式を分数の形などにして、整数の性質を用いると良い。
A〜Eの得点をそれぞれa〜eとすると、問題の条件より次の式が成り立つ。
e
a=─ ……(1)式
3
e
b=─ ……(2)式
5
3
c=─e ……(3)式
2
a+b+c+21
d=──────── ……(4)式
2
まず(1)式より判断できるのは、eは3で割り切れなければaは整数とならないから、eは3の倍数であるということである。同様に(2)式よりeは5の倍数、(3)式よりeは2の倍数でもある。つまりeは3×5×2=30の倍数でなければならない。
ここでeは30点60点90点の3通りが考えられるので、それぞれについて検討してみる。
i)e=30点の時
(1)式より、a=10点。(2)式より、b=6点。(3)式より、c=45点。
よって(4)式より、d=41となって、成り立つ。
ii)e=60点の時
同様にして、a=20点、b=12点、c=90点。よって(4)式より、整数となるdの点数は存在しない。
iii)e=90点の時
(3)式より、c=135点となって、100点を越えてしまうので、条件に反する。
∴ e=30点
[問題]5で割ると4余り、6で割ると5余り、7で割ると6余る最小の自然数の各けたの数の和はいくらか。
1.11
2.12
3.13
4.14
5.15
正答 1
反対から見ると問題が非常に簡単になることがある。これもその一つ。
5で割ると4余るということは、5で割ると1足りないということ。
6で割ると5余るということは、6で割ると1足りないということ。
7で割ると6余るということは、6で割ると1足りないということである。
つまり、問題の数は5で割っても6で割っても7で割っても1足りない数、つまり5と6と7の最小公倍数から1を引いたものである。5、6、7は共通の因数を持たないから、最小公倍数は、
5×6×7=210
より、条件に当てはまる数は
210−1=209
∴ 2+0+9=11
発展問題に挑戦!
さて問題が次のようになると、どうですか?
〔発展問題1〕5で割ると4余り、6で割ると5余る3けたの自然数のうち、最小のものの各けたの数の和はいくらか。
1.11
2.12
3.13
4.14
5.15
〔発展問題1〕正答 1
先程の問題と同様に、5と6の公倍数から1を引いたもののうち、3けたであって、しかも最小の数を求めることになる。よって、最小公倍数は30であるから、
30×4−1=120−1=119
が条件に当てはまる数である。よって、
1+1+9=11
〔発展問題2〕5で割ると4余り、6で割ると3余る3けたの自然数のうち、最小のものの各けたの数の和はいくらか。
1.11
2.12
3.13
4.14
5.15
〔発展問題2〕正答 2
反対から見ても、「5で割ると4余る」は「5で割ると1足りない」、「6で割ると3余る」は6で割ると3足りない」となって、とたんに手掛かりが無くなります。
では実際に条件に当てはまる数を挙げて見ましょう。
5で割ると4余る …… 4 9 14 19 24 29 34 39 44 49 54 59 64 69
6で割ると3余る …… 3 9 15 21 27 33 39 45 51 57 63 69 75 81
以上から条件に当てはまるのは、9、39、69であることが分かります。ここで何か気がつきませんか?
そう!
9に始まって30、つまり5と6の最小公倍数ずつ増えているのです。
この手の問題では、条件に当てはまる数が、最小公倍数に等しい間隔で、規則的に現れるということなのです。
ですから、3けたの数で最も小さいものは、129となります。
∴ 1+2+9=12
ホームヘージへ戻る… 「頻出問題の解法セミナー」へ戻る…
確 率
〔問題〕5枚のコインがある、この5枚のコインの表には1〜5の数字が1つずつ、裏にはすべて1が書かれている。いま、これらのコインを同時に投げて、出た5つの数字をすべて掛け合わせる。掛け合わせた結果の数が60の約数になる確率はいくらか。
9
1.──
16
11
2.──
16
23
3.──
32
3
4.──
4
25
5.──
32
〔正 答〕 4
60を素因数分解すると、
60=2×2×3×5
となる。ここで1、2、3、4(=2×2)、5が全て含まれており、一見、5枚のコインを投げて出た数を全て掛け合わせると、必ず60の約数になるように思うが、そうではない。
約数は元の数と同じ素因数だけを含むが、含む素因数の個数は、元の数に含まれている個数以下である。つまりこの問題で約数が含む素因数の個数は、2は2個以下、3は1個以下、5は1個以下となる。コインに書かれている数で3と5は1つずつしかないので、この条件を満たしており、これが表裏のいずれが出ても必ず60の約数でなくなるということはない。また1のコインは元々表裏のいずれが出ても約数にならないということはない。ところが2と4は、いずれか一方だけが表になれば問題はないのだが、両方同時に表になると、
2×4=2×2×2
を含むことになってしまい、60の約数ではなくなる。
問題は「60の約数である確率はいくらか」ということであるから、逆に「60の約数でない確率」を求めて1から引けばよいことになる。
コインの2と4が表の場合、他の3つのコインの出方は2×2×2(=8)通りある。ところでコインは5枚であるから、コインの全ての表裏の出方は2×2×2×2×2(=32)通りである。
8 1
60の約数でない確率=──=──
32 4
1 3
∴ 60の約数である確率=1−──=──
4 4
※別解
後半部分を「60の約数でない確率を求めて1から引く」方法ではなく直接求める。
1、3、5のコインは、表裏のいずれでも良いから、その出方は、
2×2×2=8通り
ここで2と4については場合分けをする。
i)2と4の両方が同時に表になる場合
これは約数にならないので、0通り。
ii)2か4のうちいずれか一方だけが表になる場合
2が表の場合と4が表の場合の2通り。
iii)2と4の両方が同時に裏になる場合
これは約数になる。1通り。
∴ 60の約数となるコインの出方=8×(2+1)=24通り
コインの全ての表裏の出方は2×2×2×2×2(=32)通りであるから、
24 3
60の約数である確率=──=──
32 4
時間・距離・速さ
〔問題 〕X氏は、毎日同じ時刻に駅に到着し、その時間にちょうど着くよう家から迎えに来ている自動車に乗って帰宅する。ある日X氏はいつもより早く駅に着いたので、迎えを待たずに家に向かって歩き始めたところ、途中のA地点で迎えの自動車とすれ違った。もしここで車がX氏に気づいていれば、いつもより30分早く家に帰ることが出来たのであるが、あいにく車はX氏に気づかず通りすぎ、いつもの通りに駅に向かった。X氏はA地点からさらに35分歩いたとき、駅に着いてすぐに引き返してきた車が追いつき、X氏はそこから車に乗り、結局いつもと同じ時間に家に着いた。X氏の歩く速度と自動車の走る速度の比はいくらか。ただし、自動車の速度およびX氏の歩く速度は常に一定であり、自動車に乗り込む時間は無視できるものとする。(国家II種 平成5年)
歩く速度 自動車の速度
1. 1 : 5
2. 1 : 6
3. 1 : 7
4. 1 : 8
5. 1 : 9
〔解答・解説 〕正答 3
A地点でX氏に気がついて、そこで自動車に乗って家に帰った場合、車はA地点から駅そして再びA地点に行くまでの道程を短縮することになる。この短縮された時間が30分である。(これがポイントで、後から重要な意味を持つ!)
自動車がX氏に追いついた所をB地点とすると、X氏はA地点からB地点まで35分かかっている。ところで、自動車は初めにX氏とA地点ですれ違ってから駅に行き、すぐに引き返してA地点を通ってB地点でX氏に追いついたことになる。つまり、自動車は30分でA地点に戻り、さらに5分でB地点に着いたことになる。よって、X氏は35分かかる道程を自動車は5分で走ったことになる。
1 1 1 1
∴ X氏の速度:自動車の速度=── :─ =─:─=1:7
35 5 7 1
最短経路
[問題]
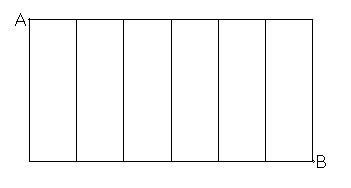
図のような道がある。A地点からB地点まで同じ道を2回通ることなく行く方法は何通りあるか。ただし、必ずしも最短経路を通らなくても良いものとする。
1.61通り
2.62通り
3.63通り
4.64通り
5.65通り
[解答]正答 4
この図において、もし横方向の2本の道を右から左に逆進する進み方を含んでAからBに行こうとすると、どのような行き方をしても必ず同じ道を通ることになる。したがって問題の条件のように進むためには、横方向の道は必ず左から右に進まなければならない。
ここで縦の道を境界として6つのブロックに分割して考える。
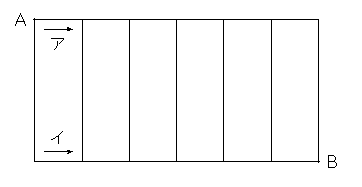
どのブロックにおいても、横方向の道は、上(図のア)を通る場合と下(図のイ)を通る場合の2通りしかない。また、どちらを通るかがきまれば、縦方向の道も通り方が一つ決まる。つまり、6つのブロックそれぞれに2通りの進み方があるということになるから、
2×2×2×2×2×2=64通り
※別解(コンピュータが好きな方へ)
実際にどのように進むかをいくつか図に書いてみると、例えば次のようになる。

さて、これはどこかで見たことがあるように感じます。そう!コンピュータや様々な電子機器に出てくるデジタル信号に良く似ています。
この問題ではビット数は6です。よって、
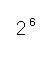 =64通り
=64通り
こんな方法でも解けます。
ホームページへ戻る… 頻出問題の解法セミナー…




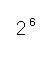 =64通り
=64通り